
Four points are marked and labeled with their coordinates: (2, 3) in green, (−3, 1) in red, (−1.5, −2.5) in blue, and the origin (0, 0) in purple. We will love to hear from you.Illustration of a Cartesian coordinate plane.
#Abscissa definition chemistry free
If you have any queries or suggestions, feel free to write them down in the comment section below. We hope this article on coordinates has provided significant value to your knowledge. Some other helpful articles by Embibe are provided below: Foundation Concepts What is abscissa and ordinates in coordinate geometry?Īns: Abscissa is the \(x\)-coordinate and ordinate is the \(y\)-coordinate. How do you write the coordinates of a point?Īns: We always write coordinates in brackets, with the two numbers separated by comma. Coordinates are ordered pairs of numbers the first number represents the point on the \(X\)-axis and the second the point on the \(Y\)-axis. To map geographical locations using latitudes and longitudes.Īns: The location of any point on a plane is expressed by an ordered pair of values \((x,\,y)\) and these pairs are known as the coordinates. To determine the position and location of aeroplanes accurately in aviation.Ĥ. To locate the position of cursor or finger in digital devices like computers, mobile phones, etc.Ģ. Therefore, the coordinates of the origin are \((0,\,0)\).Īns: Coordinate geometry has various applications in real life. Q.1. What are the coordinates of the origin \(0\)?Īns: It has zero distance from both the axes so its abscissa and ordinate are both zero.
#Abscissa definition chemistry how to
Also, we have seen how to represent coordinates in \(3\) – dimensional plane. We have also discussed the types of coordinate systems like the cartesian and the polar coordinate system. The abscissa is the \(x\)- coordinate, and the ordinate is the \(y\)-coordinate. In this article, we have discussed that we use coordinates to locate the point in the plane and it is always written in the ordered pair like we write \(x\)-coordinate in the first position and \(x\)-coordinate in the second position. Hence, the coordinates of \(x\) are _,_.Īns: The point \(P\) is at \(-3\) units from \(X\)-axis, and the \(y\) and \(z\)-coordinates are zero. The \(x\)-coordinate and the \(y\)-coordinate of the point \(S\) are _ and _, respectively. Hence, the coordinates of \(L\) are _,_.Ĥ. The \(x\)-coordinate and the \(y\)-coordinate of the point \(L\) are _ and _, respectively. Hence, the coordinates of \(M\) are _,_.ģ. The \(x\)-coordinate and the \(y\)-coordinate of the point \(M\) are _ and _, respectively. Hence, the coordinates of \(B\) are _,_.Ģ. The abscissa and the ordinate of the point \(B\) are _ and _, respectively. See the figure given below and complete the following statements:ġ. The distance from the pole is called the radial distance or simply radius and the angular coordinate, polar angle.Ĭonsider the figure below that shows the relationship between polar and cartesian coordinates. Thus, a point in the polar coordinate system is represented as a pair of coordinates \((r,\,\theta )\). The point will have a unique distance from the origin \(r\). The angle \(\theta \) with the polar axis has a single line through the pole measured anti-clockwise from the axis to the line. Basically, we have two parameters, namely angle and radius. The polar coordinate system is a different way to express points in a plane.
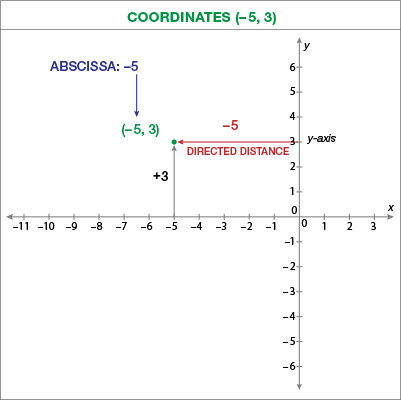
The \(y\)-coordinate of a point is its perpendicular distance from the \(X\)-axis measured along the \(Y\)-axis, and it is known as ordinate. The \(x\)-coordinate of a point is its perpendicular distance from the \(Y\)-axis measured along the \(X\)-axis, and it is known as abscissa.


 0 kommentar(er)
0 kommentar(er)
